Limits and Derivatives Problem Set
Answer the following questions to the best of your ability. Attempt exercises on your own first to make sure you fully understand the concepts. Feel free to work with anyone in the cohort after giving the problems a try!
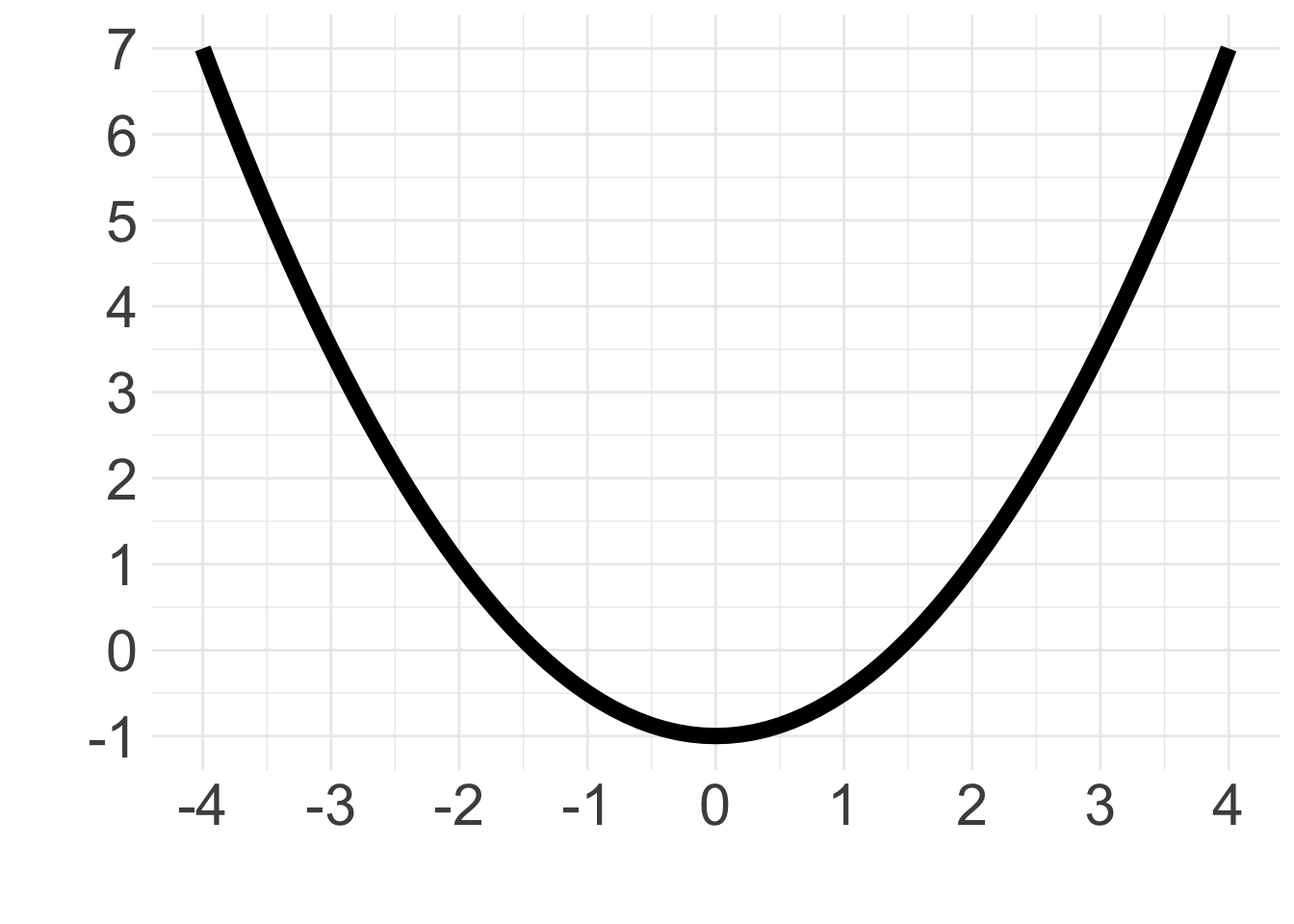
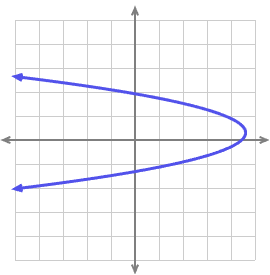
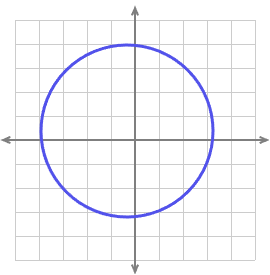
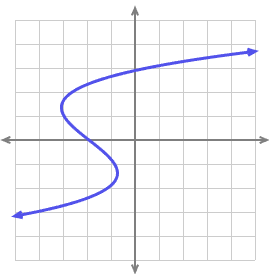
- Which of these graphs depict functions and which do not?
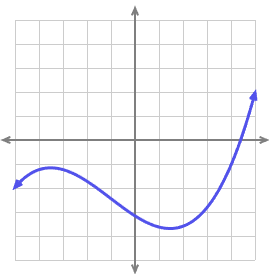
- Investigate what is the value of the following limits:
\[ \lim_{x\to -2^-}\frac{4x}{x+2} \]
\[ \lim_{x\to 3}2^x \]
- Determine the value of \(b\) to make \(h(x)\) continuous at \(x=-3\). Explain your reasoning using limits.
\[ h(x)=\begin{cases} bx^2-\frac{3}{2}x-5 &x<-3 \\ -2x-9 &x\ge-3 \end{cases} \]
- Let \(f(x) = 2x^2+4\). Calculate \(f'(x)\) and \(f'(-3)\).
- Calculate the derivative of \(g(x) = x^4-5x^3+x-5\) at \(x=5\).
- What is the instantaneous rate of change of \(h(x) = \frac{5}{x^2}\) at \(x=2\)?
Approximate the slope of the tangent line in the graph below at \(x=2\).
Write a short paragraph describing how the slope of the tangent line represents the derivative.