Limits and Derivatives Problem Set Solutions

Answer the following questions to the best of your ability. Attempt exercises on your own first to make sure you fully understand the concepts. Feel free to work with anyone in the cohort after giving the problems a try!

1. Which of these graphs depict functions and which do not?

Graphs A,B, and C all fail the vertical line test. Thus they are not functions. Graph D is a function because passes the vertical line test and thus is a function.

2. Investigate what is the value of the following limits:

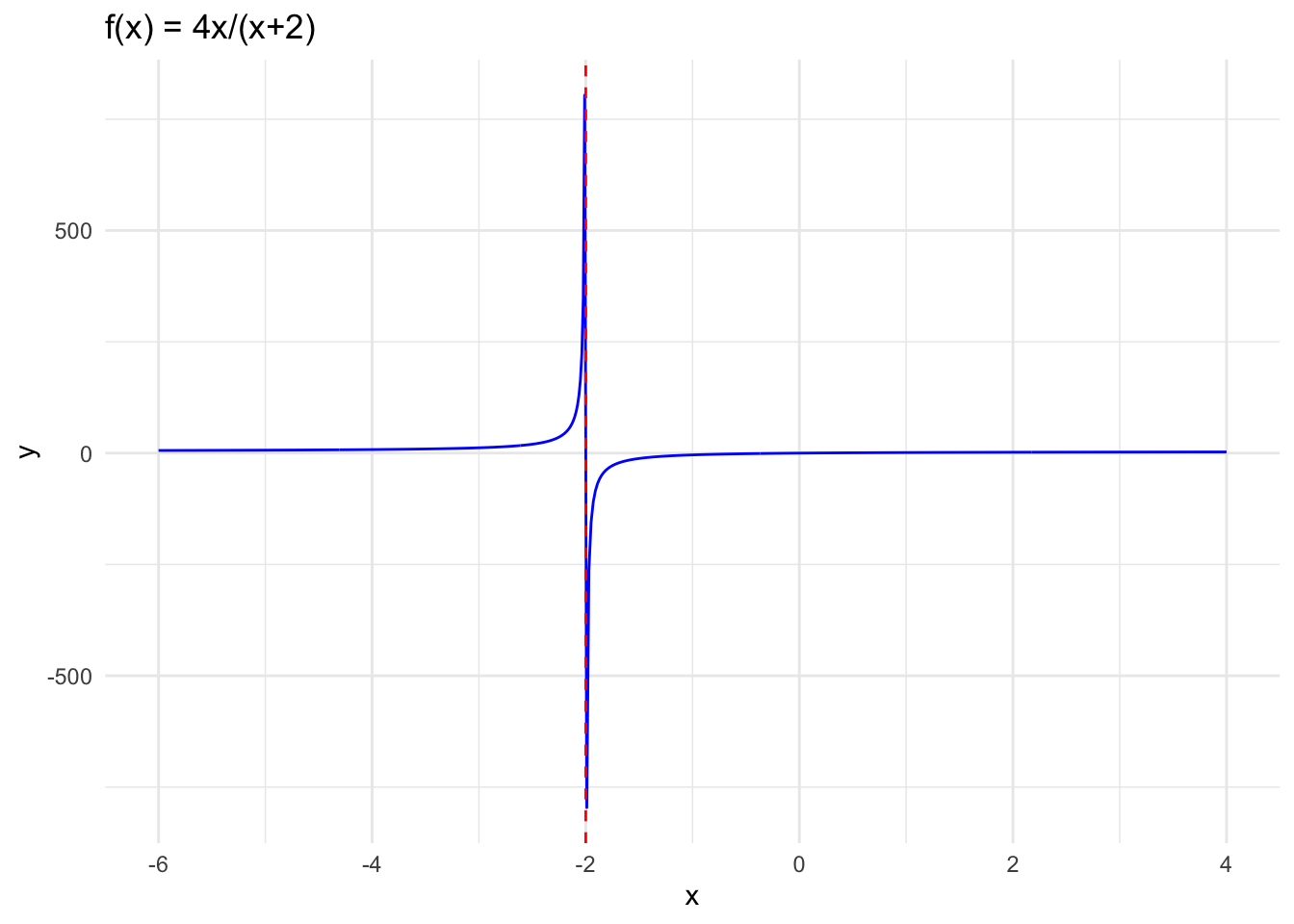
\[ \lim_{x\to -2^-}\frac{4x}{x+2} \]

To investigate this limit we can evaluate the function \(\frac{4x}{x+2}\) from the left with values getting closer to -2. We can see from the approximation below that \(y = \frac{4x}{x+2}\) rapidly increases with values closer to -2. So, we can say the limit goes to infinity.

x	-2.5	-2.1	-2.01	-2.001	-2.0001	-2.00001
y	20.0	84.0	804.00	8004.000	80004.0000	800003.99999

We can also plot the function to have a visual understanding of its behavior near -2.

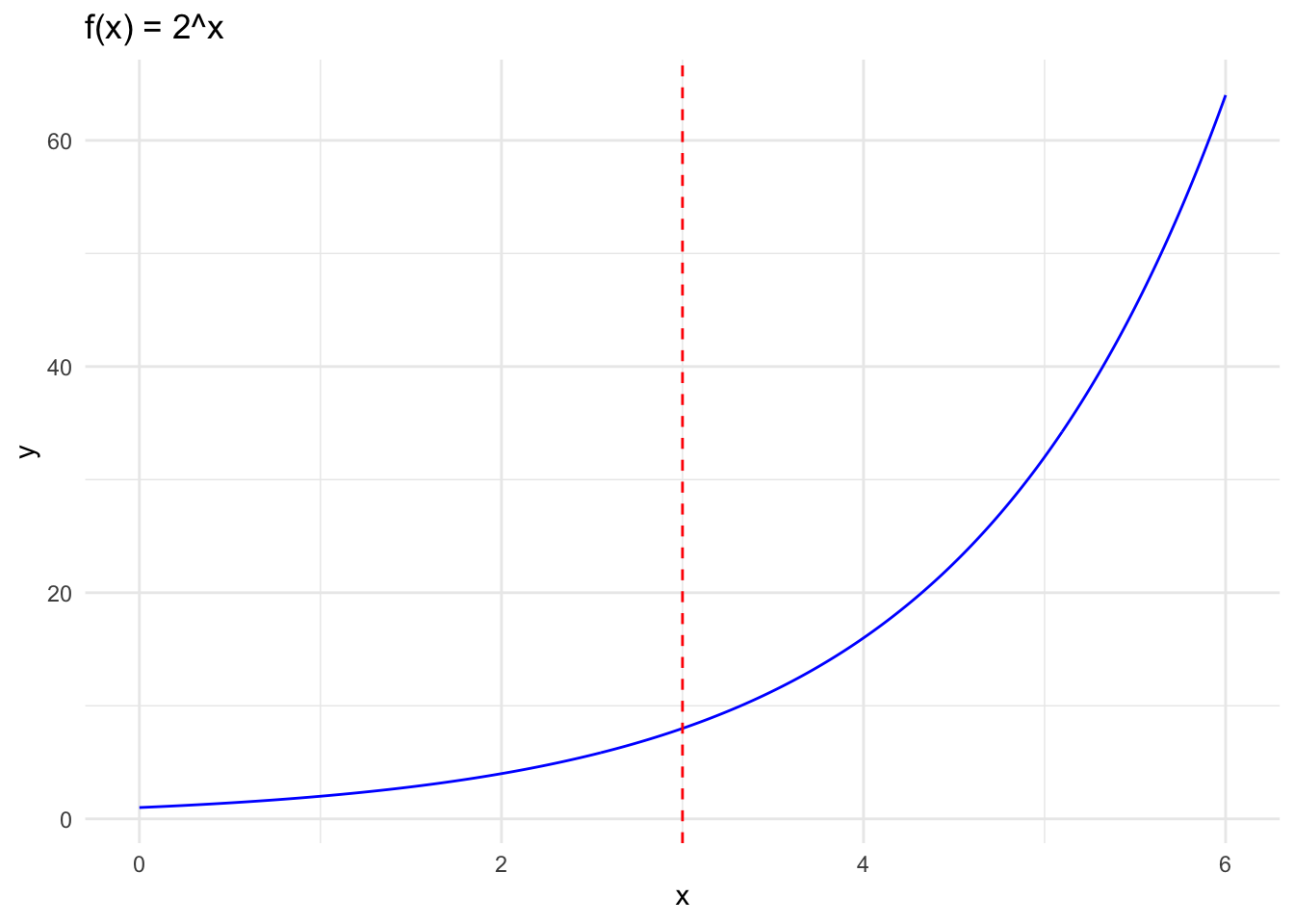
\[ \lim_{x\to 3}2^x \]

To investigate this limit we can evaluate the function \(2^x\) with values of \(x\) approaching 3 from the left and the right. The table below shows that the limit approaches 8 at x=3 from both directions, so we can say \(\lim_{x\to 3}2^x=8\).

x	2.500000	2.900000	2.99000	2.999000	3.001000	3.010000	3.100000	3.50000
y	5.656854	7.464264	7.94474	7.994457	8.005547	8.055644	8.574188	11.31371

We can also graph this function and see it is continuous. So \(\lim_{x\to 3}2^x = 2^3 = 8\).

3. Determine the value of \(b\) to make \(h(x)\) continuous at \(x=-3\). Explain your reasoning using limits.

\[ h(x)=\begin{cases} bx^2-\frac{3}{2}x-5 &x<-3 \\ -2x-9 &x\ge-3 \end{cases} \]

This function is broken down into two “pieces”: it equals \(bx^2 - \frac{3}{2}x - 5\) when \(x\) is less than -3, and it equals \(-2x-9\) when \(x\) is greater or equal to -3. To connect these two pieces and make \(h(x)\) continuous we need both pieces to approach the same value at \(x=-3\). In other words, we need that

\[ -3 = h(x) = \lim_{x\to-3} h(x).\]

Let’s calculate the side limits to see what’s going on with \(\lim_{x\to-3} h(x)\). From the left-hand side we have that

xw \[\lim_{x\to-3^-} h(x) = \lim_{x\to-3^-} bx^2 - \frac{3}{2}x - 5 = 9b + \frac{9}{2}.\]

a8670390NCEAS

From the right-hand side we have that

\[ \lim_{x\to-3^+} h(x) = \lim_{x\to-3^+} -2x-9 = -3 \]

If we want \(h(x)\) to be continuous at \(x=-3\) we then need

\[ -3 = h(x) = \lim_{x\to-3^-} h(x) = \lim_{x\to-3^+} h(x) = 9b + \frac{9}{2} \]

Solving this equation we obtain that

\[ \begin{align} 9b=\frac{-5}{2}\\ b=\frac{-5}{18}. \end{align} \]

4. Let \(f(x) = 2x^2+4\). Calculate \(f'(x)\) and \(f'(-3)\).

\[\begin{align} f(x) &= 2x^2+4\\ f'(x) &= 4x\\ f'(-3) &=4(-3)\\ &=-12 \end{align}\]

5. Calculate the derivative of \(g(x) = x^4-5x^3+x-5\) at \(x=5\).

\[\begin{align} g(x) &= x^4-5x^3+x-5 \\ g'(x) &= 4x^3-15x^2+1 \\ g'(5) &= 4(5)^3-15(5)^2+1\\ &=126 \end{align}\]

6. What is the instantaneous rate of change of \(h(x) = \frac{5}{x^2}\) at \(x=2\)?

We have that

\[ h(x) = \frac{5}{x^2} = 5x^{-2} \]

Then,

\[\begin{align} h'(x) & =-10x^{-3}\\ h'(2) &= -10(2)^{-3}\\ & = -\frac{10}{8}\\ &=-1.25. \end{align}\]

1. Approximate the slope of the tangent line in the graph below at \(x=2\).

2. Write a short paragraph describing how the slope of the tangent line represents the derivative.

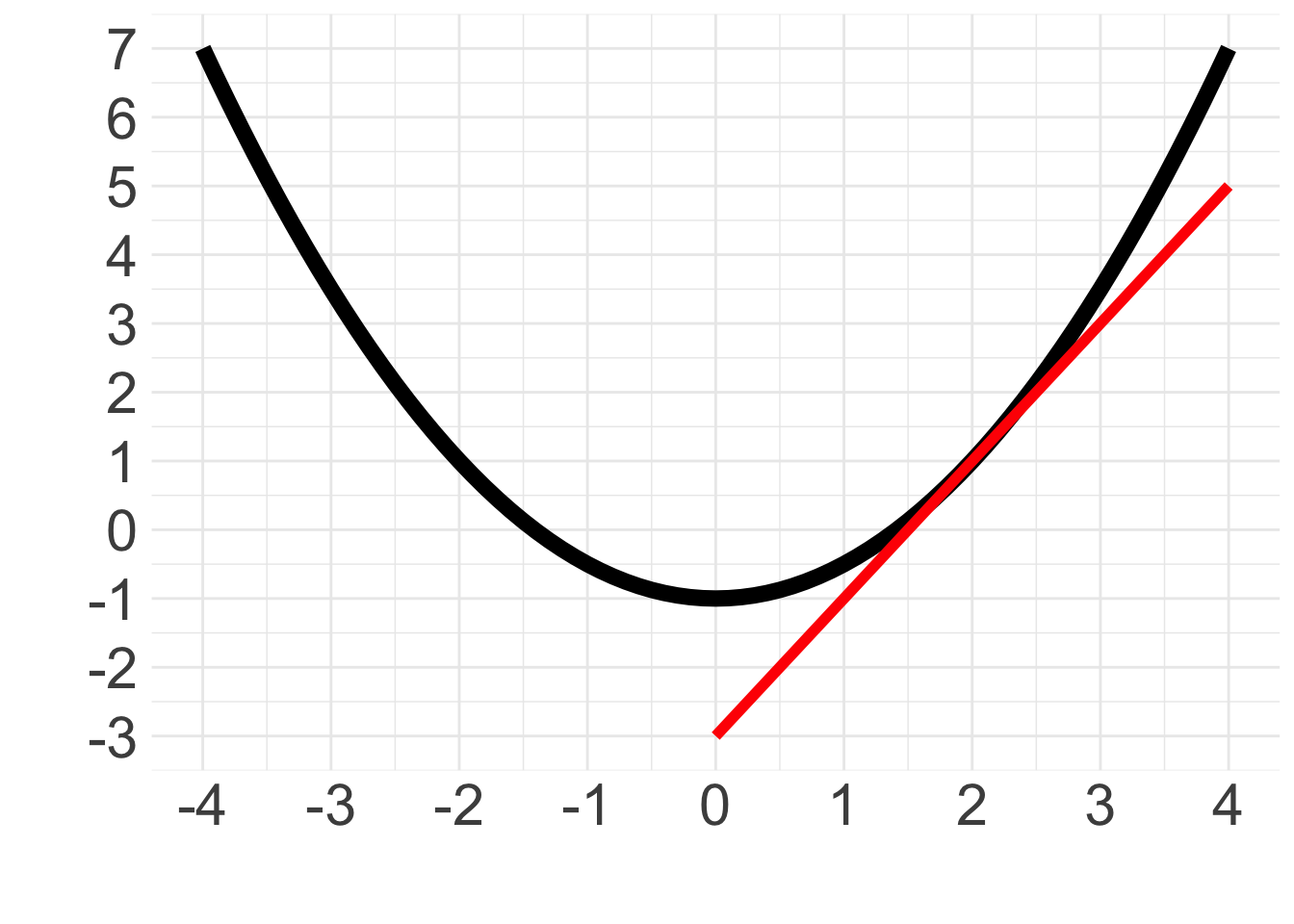
a. First, we draw a tangent line to the graph at \(x=2\), this is the red line plotted with the graph.

Using rise over run we can take two points on the tangent line to find the slope. Let’s use \((2,1)\) and \((1,-1)\) as our points on the tangent, then

\[ slope=\frac{1- (-1)}{2-1}=2. \]

b. The tangent line provides the slope or instaneous rate of change at single point along the curve. Therefore the slope of the tangent line is the derivative.